L'accumulation de nutriments (comme le phosphore ou l'azote) dans l'eau d'un lac peut amener un changement d'état qui s'accompagne de prolifération d'algues, de dégradation de la qualité de l'eau et de la biodiversité, éventuellement de bloom bactérien : c'est l'eutrophisation. Le problème du lac et des exploitations riveraines consiste à déterminer s'il est possible de concilier la pratique d'une activité qui apporte des nutriments et la conservation du lac dans un état souhaitable (oligotrophe, par opposition à eutrophe).
Ce problème est décrit en détail dans :
S. Martin. The cost of restoration as a way of defining resilience: a viability approach applied to a model of lake eutrophication. Ecol. Soc. http://www.ecologyandsociety.org/vol9/iss2/art8
On souhaite que les apports $L$ soient supérieurs à un seuil $L_{min}$, pour tenir compte des besoins de l'activité des exploitations riveraines ; et que la concentration du phosphore total $P$ soit inférieure à un seuil $P_{max}$ pour conserver le lac oligotrophe. Ces états souhaitables constituent l'ensemble de contraintes $K=[L_{min}, +\infty[ \times [0,P_{max}]$.
L'évolution de la concentration du phosphore total dans le lac est modélisée par une pseudo-sygmoïde :
$$\frac {dP} {dt}=-bP(t)+L(t)+r\frac {P(t)^{q}} {m^{q} + P(t)^{q}} \qquad$$
On suppose que l'évolution des apports de phosphore peut être contrôlée (par des unités de dépollution, la mise en place de zones humides, le changement de pratique agricoles ou industrielles, etc.) et on modélise ces contrôles par une grandeur unique $u\in U=[u_min,u_max]$. La dynamique des apports est modélisée par :
$$\frac {dL} {dt}=u \in [- u_{min}, u_{max}] \qquad$$
Le problème de viabilité est donc défini par :
\begin{equation} \label{eq:systemlac}
(P)\left\{
\begin{array}{l}
\frac{dL}{dt}=u\in U=\left[ u_{min},u_{max}\right] \\
\frac{dP}{dt}=-b P(t) + L(t) +r\frac{P(t)^{q}}{m^{q} + P(t)^{q}} \\
\left(L(t),P(t)\right) \in K=[L_{min}, +\infty[ \times [0,P_{max}]
\end{array}
\right.
\end{equation}
Le noyau de viabilité peut être obtenu par le calcul d'une courbe intégrale (voir page 22 de https://arxiv.org/pdf/2107.02684 ). La figure suivante montre le résultat pour les paramètres suivants : $b=1,95$ an$^{-1}$ ; $q=1,9$ ; $m=19,44\ \mu gl^{-1}$; $r=72,22\ \mu gl^{-1}$ an$^{-1}$; $L_{min}=1,25\ \mu gl^{-1}$ ; $P_{max}=17,39\ \mu gl^{-1}$ ; $|u_{min}|=u_{max}=3,15$.
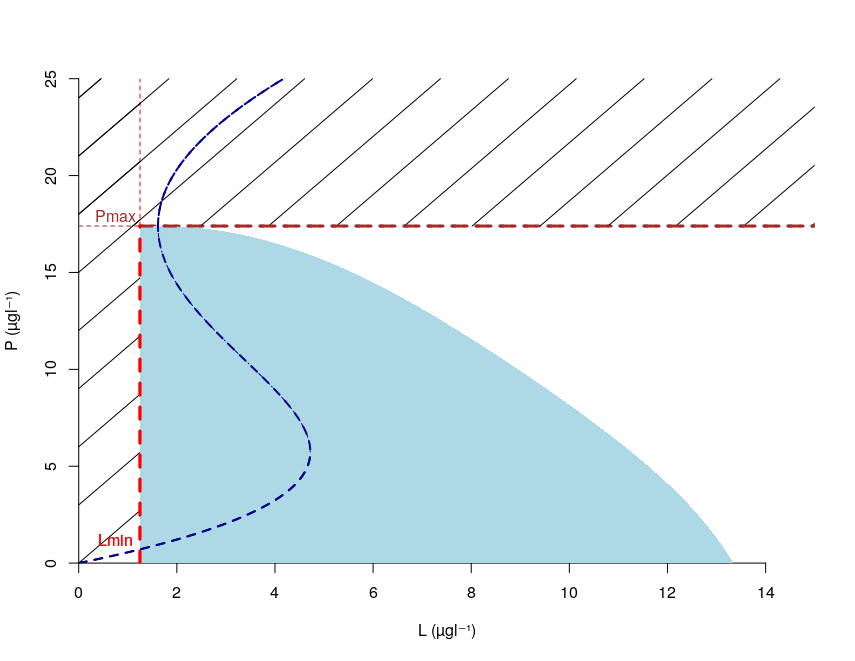
Une approximation peut être calculée directement avec des logiciels de calcul de noyau comme ViabLab.
Pour la release 1 de ViabLab, voici les codes utilisés correspondants à l'exemple développé ci-dessus.
Fichier .json (à placer dans le répertoire VIABLAB/INPUT) : Lac_params.json
Fichier .h (à placer dans le répertoire VIABLAB/source/data : data_Lac.h
Ces fichiers correspondent aux paramètres suivants : $b=0.8$ an$^{-1}$ ; $q=8$ ; $m=1\ \mu gl^{-1}$; $r=1\ \mu gl^{-1}$ an$^{-1}$; $L_{min}=0.1\ \mu gl^{-1}$ ; $P_{max}=1.4\ \mu gl^{-1}$ ; $|u_{min}|=u_{max}=0.09$.