Dans le cas où $\phi$ est un polynôme, l'ensemble de Julia rempli est le complémentaire du bassin d'attraction du point à l'infini; autrement dit, ce sont les points dont l'orbite est bornée.
$\phi$Étant donnés un nombres complexes, $u:=a+ib$, soit la fonction complexe $\phi(z)=z^2+c$ ou de manière équivalente, la fonction $\phi(x,y):=(x^2-y^2+a,2xy+b)$ avec $z=x+iy$, on considère la suite $(z_n)$ définie par la relation de récurrence : $z_{n+1}=\phi(z_n,u)$ avec $\phi(z)=z^2+c$,
Pour une valeur donnée de $u$, l'ensemble de Julia correspondant est la frontière de l'ensemble des valeurs initiales $z_0$ pour lesquelles la suite est bornée.
D'après
Aubin, J.-P., Bayen, A., & Saint-Pierre, P. Viability Theory: New Directions. Springer. 2011.
Le sous-ensemble $K_u:=Viab_{\phi}(B(0,1))$ est le sous-ensemble de Julia rempli pour la function $\phi$ et sa frontière $J_u:=\partial K_u$ est l'ensemble de Julia.
L'Algorithme de Viabilité permet donc de calculer une approximation de ces ensembles de Julia.
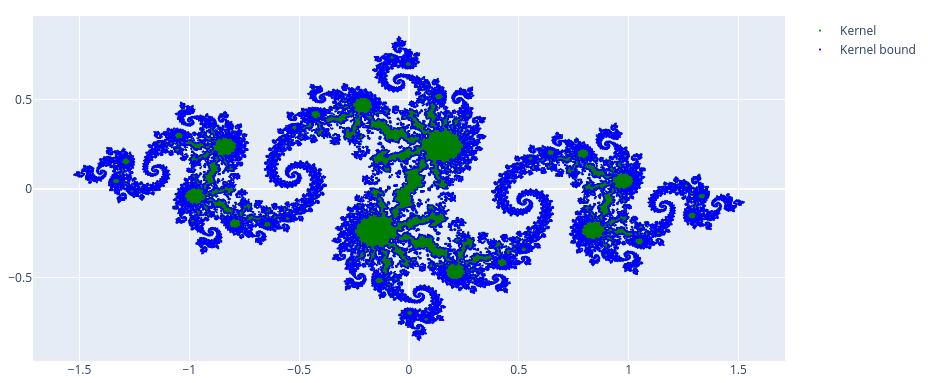
Voici le noyau de viabilité approché obtenu en utilisant le logiciel ??? :
To compute this kernel with VIABLAB 3.02, juste copy this two following files :
file julia.h
PARAMETRE1 = 12
PARAMETRE2=13
file julia.c
function dynamics {
}