Mathématique

Introduction 

The accumulation of nutrients (such as phosphorus or nitrogen) in the water of a lake can lead to a change of state that results in the proliferation of algae, the degradation of water quality and biodiversity, and possibly bacterial blooms: this is eutrophication. The problem of the lake and its riparian holdings is to determine whether it is possible to reconcile the practice of an activity which provides nutrients and the conservation of the lake in a desirable state (oligotrophic, as opposed to eutrophic).

This problem is described in detail in:

S. Martin. The cost of restoration as a way of defining resilience: a viability approach applied to a model of lake eutrophication. Ecol. Soc.   http://www.ecologyandsociety.org/vol9/iss2/art8

Nutrients inputs $L$ must be above a minimal threshold $L_{min}$, to take into account the needs of the holdings' activities; And the concentration of total Phosphorus $P$ must remain  below a threshold  $P_{max}$, to keep the lake in an oligotrophic state. These desirable states form the constraints set $K=[L_{min}, +\infty[ \times [0,P_{max}]$.

The evolution of the concentration of total phosphorus in the lake is modeled by a pseudo-sygmoid:

$$\frac {dP} {dt}=-bP(t)+L(t)+r\frac {P(t)^{q}} {m^{q} + P(t)^{q}} \qquad$$

It is assumed that the evolution of phosphorus inputs can be controlled (by decontamination units, the establishment of wetlands, changes in agricultural or industrial practices, etc.), and we model these controls by a single quantity $u\in U=[u_min,u_max]$. The dynamics of the inputs are modeled by:

$$\frac {dL} {dt}=u \in [- u_{min}, u_{max}] \qquad$$

The viabillity problem is then defined by:

\begin{equation} \label{eq:systemlac}
(P)\left\{
\begin{array}{l}
\frac{dL}{dt}=u\in U=\left[ u_{min},u_{max}\right] \\
\frac{dP}{dt}=-b P(t) + L(t) +r\frac{P(t)^{q}}{m^{q} + P(t)^{q}} \\
\left(L(t),P(t)\right) \in K=[L_{min}, +\infty[ \times [0,P_{max}]
\end{array}
\right.
\end{equation}
 

Exemple 1

The viabillity kernel can be obtained by calculating an integral curve (see page 22 in https://arxiv.org/pdf/2107.02684 ). Next figure shows the result for the following parameters:  $b=1,95$ an$^{-1}$ ; $q=1,9$ ; $m=19,44\  \mu gl^{-1}$; $r=72,22\  \mu gl^{-1}$ an$^{-1}$; $L_{min}=1,25\  \mu gl^{-1}$ ; $P_{max}=17,39\  \mu gl^{-1}$ ;   $|u_{min}|=u_{max}=3,15$.

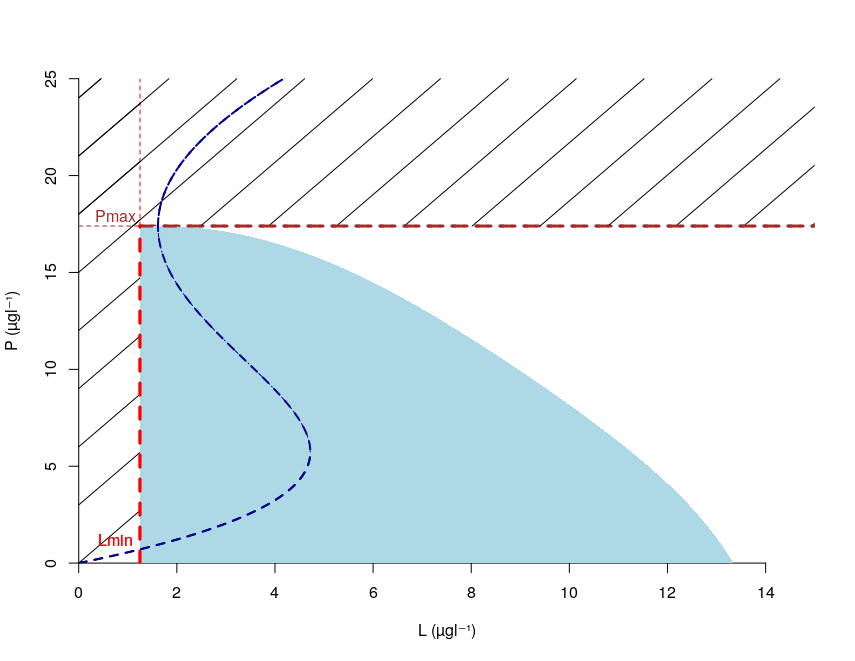In light blue the viabillity kernel. The dotted marine line shows the equilibrium curve of the system.

An approximation can be calculated directly with viability kernel calculation software such as ViabLab.

File .json (to be placed in the following repertory: VIABLAB/INPUT): Lac_params.json

File .h (to be placed in the following repertory: VIABLAB/source/data : data_Lac.h

These files correspond to the parameters: $b=0.8$ year$^{-1}$ ; $q=8$ ; $m=1\  \mu gl^{-1}$; $r=1\  \mu gl^{-1}$ year$^{-1}$; $L_{min}=0.1\  \mu gl^{-1}$ ; $P_{max}=1.4\  \mu gl^{-1}$ ;   $|u_{min}|=u_{max}=0.09$.

Le contrôle est discrétisé sur 3 valeurs étant donné les spécificités du problème.

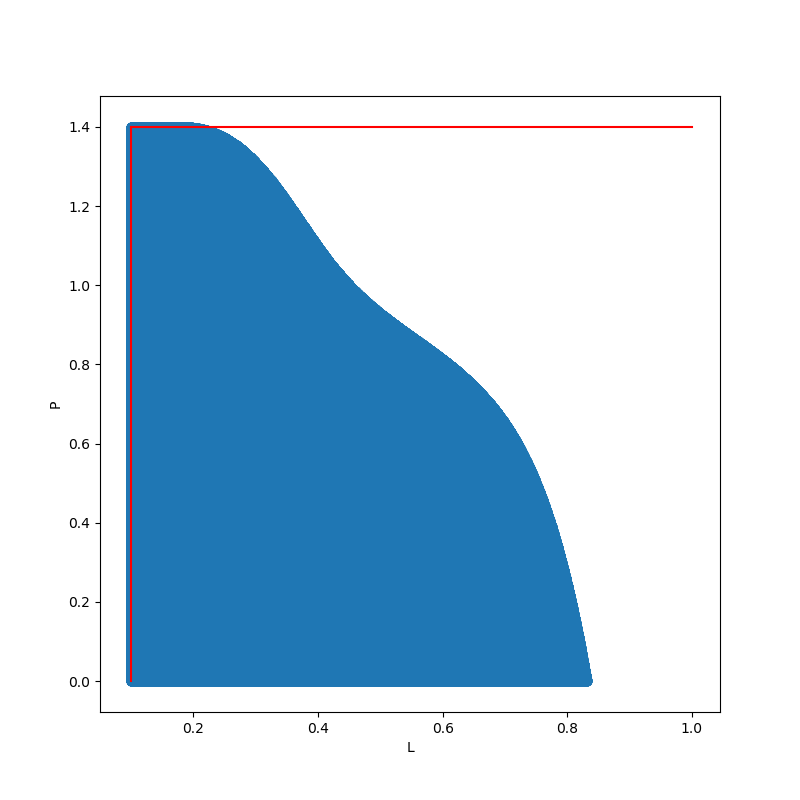
La discrétisation est faite sur 5000 points / axe. L'approximation calculée par ViabLab est montrée sur la figure suivante. En rouge les seuils des contraintes. On voit que l'approximation du noyau est bien faite par l'extérieur.

Introduction

Le problème d'eutrophisation du lac décrit comme le problème de viabilité du lac et des exploitations riveraines est traité à un niveau global et suppose un décideur unique. Dans le présent exemple les parties prenantes sont réunies dans un comité, et les membres du comité (appelés individus dans la suite) ne sont pas nécessairement d'accord sur la dynamique du lac. Cet exemple illustre les cas où la gestion est collective et où il n'y a pas de consensus sur la dynamique. Ce problème est un problème de viabilité garantie.

Ce problème est décrit en détail dans :

Alvarez, I., Zaleski, L., Briot, J.-P., Irving, M. de A. (2023). Collective management of environmental commons with multiple usages: A guaranteed viability approach. Ecological Modelling, 475, Article 110186

Version auteur disponible ici

Les caractéristiques 

Les caractéristiques du problème modélisé sont les suivantes :  

1.  $N$ individus utilisent les même variables pour décrire le système. Dans cet exemple du lac, ce sont les mêmes variables $L$ (apports de phosphore) et $P$ (concentration totale de phosphore) que dans le cas du décideur unique.
2. Les contrôles admissibles retenus dans les modèles sont communs à tous les individus. On garde donc la même variable de contrôle et les mêmes bornes : $u\in U=[u_{min},u_{max}]$.
3. Tous les individus $i$ peuvent définir un ensemble d'états souhaitables $K_i$ dont l'intersection est non vide. On garde donc un ensemble de contraintes similaires au cas du décideur unique :  $x=\left(L(t),P(t)\right) \in K=[L_{min}, +\infty[ \times [0,P_{max}]$
4. La dynamique du système est modélisée pour chaque individu par un ensemble d'équations (ou d'inclusion différentielles) $S_i$
5. L'objectif de chaque individu est de maintenir le système modélisé par leur dynamique $S_i$ dans leur ensemble d'états souhaitables $K_i$

6. Les individus acceptent de partager leurs informations personnelles avec un tiers de confiance.

   Dans cet exemple, on considère $N=4$ individus. Trois d'entre eux ($i\in\{1,2,3\}$) adoptent la dynamique classique, mais avec des paramètres différents :

   \begin{equation} \label{eq:systemlac}
   (P_i \text{ modèle 1})\left\{
   \begin{array}{l}
   \frac{dL}{dt}=u\in U=\left[ u_{min},u_{max}\right] \\
   \frac{dP}{dt}=-b_i P(t) + L(t) +r_i\frac{P(t)^{q_i}}{m_i^{q_i} + P(t)^{q_i}} \\
   \left(L(t),P(t)\right) \in K=[L_{min}, +\infty[ \times [0,P_{max}]
   \end{array}
   \right.
   \end{equation}

   Un individu ($i=4$) considère que le processus de relargage peut se produire différemment, et utilise une formule différente pour la pseudo-sygmoïde :

   \begin{equation}
   (S' \text{ modèle 0}) \quad \frac{dP}{dt}=-b_i P(t) + L(t) + r_i \frac{P(t)}{P(t) + m_i e^{(-\lambda_i(P(t)-m_i)) }}
   \end{equation}

   Les valeurs numériques pour les calculs sont les suivantes : $u_{min}=-u_{max}/2$ ; $u_{max}\approx 3,15\; \mu g.l^{-1}.\text{an}^{-1}$, $L_{min}\approx6,94 \; \mu g.l^{-1}$,  $P_{max}=24.76 \; \mu g.l^{-1}$, 

Le  tableau suivant rassemble les valeurs des paramètres pour chaque individu (b,r,m sont en $\mu g.l^{-1}$).

Les incertitudes sont traitées comme des variables prenant leur valeur dans des ensembles. Le problème est un problème de viabilité garantie, dans lequel le vecteur $v$ des "tyches" regroupent les paramètres incertains : $v_1$ représente le paramètre $b_i$, $v_2$ : $\alpha_i$, $v_3$ : $q_i$ et $v_4$ représente $\lambda_i$. La dynamique du modèle avec incertitudes devient :

\begin{equation}
f_v(x=(L,P),u,v)=\left( 
\begin{array}{l}
u\\
- v_1 P + L +  r \left( (1-v_2) \frac{P^{v_3}}{m^{v_3} + P^{v_3}} + v_2 \frac{P}{P + m e^{(-v_4(P-m)) }}\right)  \;
\end{array}
\right)
\end{equation}

Problèmes

Le problème de viabilité garantie qui doit être résolu est le suivant :

\begin{equation}
(P_v)\left\{
\begin{array}{lcl}
(L,P)'(t)&=&f_B((L,P)(t),u(t),v(t))\\
u(t)&\in& U=\left[ u_{min},u_{max}\right] \\
v(t)&\in & V=[2.2,2.3]\times[0,1]\times[2.2,2.3]\times[1/19,1/18]\\
(L,P)(t) &\in& K \; 
\end{array}
\right.
\end{equation}

Le noyau garanti peut être approximé avec ViabLab (version 2.2). Le code correspondant est ici : https://forgemia.inra.fr/isabelle.alvarez/emlake

Introduction 

The accumulation of nutrients (such as phosphorus or nitrogen) in the water of a lake can lead to a change of state that results in the proliferation of algae, the degradation of water quality and biodiversity, and possibly bacterial blooms: this is eutrophication. The problem of the lake and its riparian holdings is to determine whether it is possible to reconcile the practice of an activity which provides nutrients and the conservation of the lake in a desirable state (oligotrophic, as opposed to eutrophic).

This problem is described in detail in:

S. Martin. The cost of restoration as a way of defining resilience: a viability approach applied to a model of lake eutrophication. Ecol. Soc.   http://www.ecologyandsociety.org/vol9/iss2/art8

Nutrients inputs $L$ must be above a minimal threshold $L_{min}$, to take into account the needs of the holdings' activities; And the concentration of total Phosphorus $P$ must remain  below a threshold  $P_{max}$, to keep the lake in an oligotrophic state. These desirable states form the constraints set $K=[L_{min}, +\infty[ \times [0,P_{max}]$.

The evolution of the concentration of total phosphorus in the lake is modeled by a pseudo-sygmoid:

$$\frac {dP} {dt}=-bP(t)+L(t)+r\frac {P(t)^{q}} {m^{q} + P(t)^{q}} \qquad$$

It is assumed that the evolution of phosphorus inputs can be controlled (by decontamination units, the establishment of wetlands, changes in agricultural or industrial practices, etc.), and we model these controls by a single quantity $u\in U=[u_min,u_max]$. The dynamics of the inputs are modeled by:

$$\frac {dL} {dt}=u \in [- u_{min}, u_{max}] \qquad$$

The viabillity problem is then defined by:

\begin{equation} \label{eq:systemlac}
(P)\left\{
\begin{array}{l}
\frac{dL}{dt}=u\in U=\left[ u_{min},u_{max}\right] \\
\frac{dP}{dt}=-b P(t) + L(t) +r\frac{P(t)^{q}}{m^{q} + P(t)^{q}} \\
\left(L(t),P(t)\right) \in K=[L_{min}, +\infty[ \times [0,P_{max}]
\end{array}
\right.
\end{equation}
 

Exemple 1

The viabillity kernel can be obtained by calculating an integral curve (see page 22 in https://arxiv.org/pdf/2107.02684 ). Next figure shows the result for the following parameters:  $b=1,95$ an$^{-1}$ ; $q=1,9$ ; $m=19,44\  \mu gl^{-1}$; $r=72,22\  \mu gl^{-1}$ an$^{-1}$; $L_{min}=1,25\  \mu gl^{-1}$ ; $P_{max}=17,39\  \mu gl^{-1}$ ;   $|u_{min}|=u_{max}=3,15$.

Noyau de viabilité du problème du lac et des exploitations riveraines. In light blue the viabillity kernel. The dotted marine line shows the equilibrium curve of the system.

An approximation can be calculated directly with viability kernel calculation software such as ViabLab.

File .json (to be placed in the following repertory: VIABLAB/INPUT): Lac_params.json

File .h (to be placed in the following repertory: VIABLAB/source/data : data_Lac.h

These files correspond to the parameters: $b=0.8$ year$^{-1}$ ; $q=8$ ; $m=1\  \mu gl^{-1}$; $r=1\  \mu gl^{-1}$ year$^{-1}$; $L_{min}=0.1\  \mu gl^{-1}$ ; $P_{max}=1.4\  \mu gl^{-1}$ ;   $|u_{min}|=u_{max}=0.09$.

Le contrôle est discrétisé sur 3 valeurs étant donné les spécificités du problème.

La discrétisation est faite sur 5000 points / axe. L'approximation calculée par ViabLab est montrée sur la figure suivante. En rouge les seuils des contraintes. On voit que l'approximation du noyau est bien faite par l'extérieur.