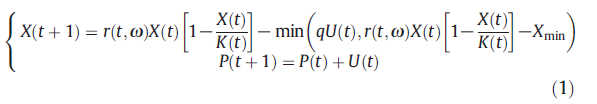Modélisation des capacités des agrosystèmes diversifiés à faire face à l’incertitude
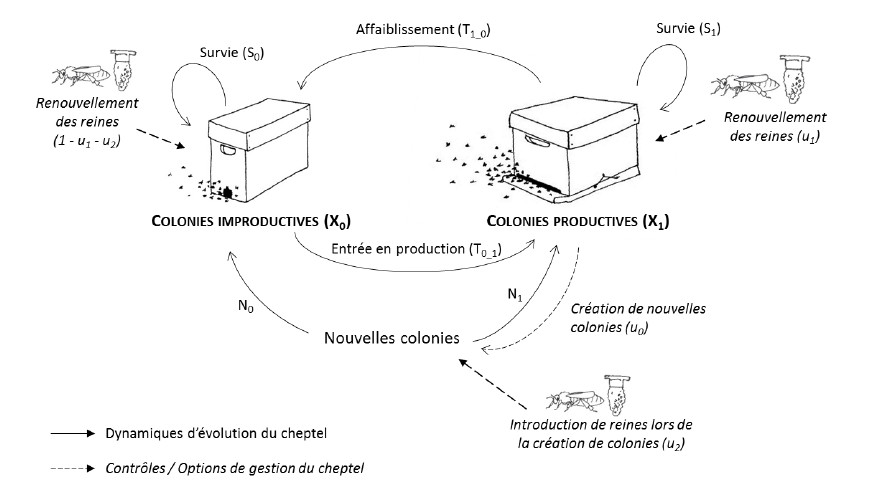
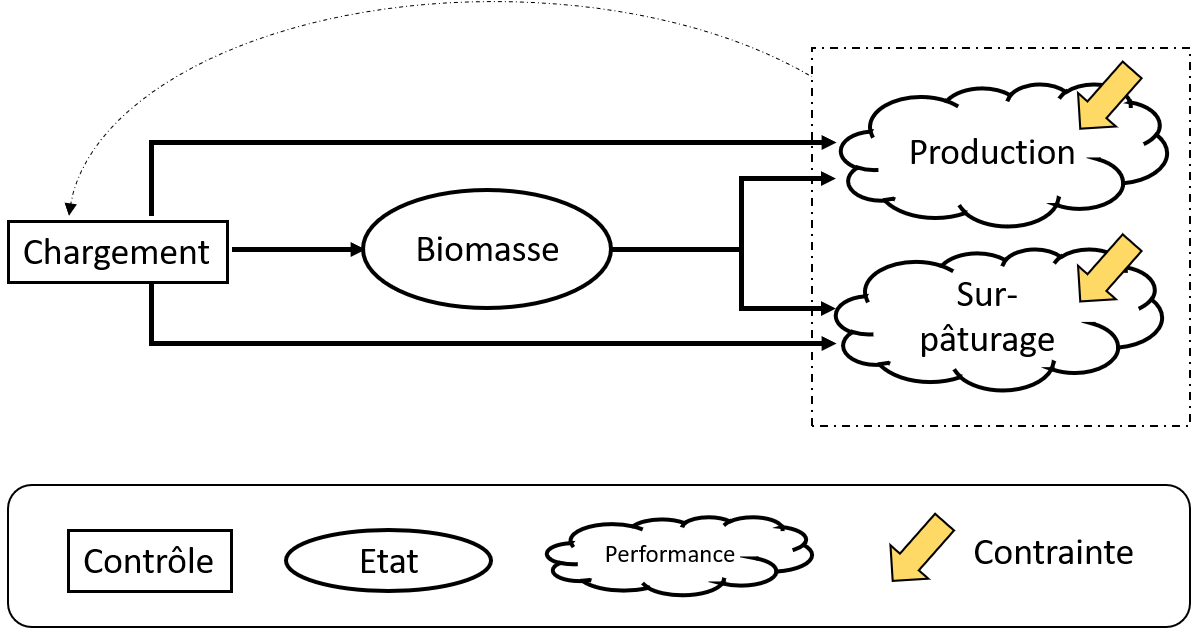
En remettant les processus écologiques au cœur des dynamiques de production, les systèmes agricoles écologisés doivent composer avec de nombreuses incertitudes. La résilience, l’adaptabilité et la flexibilité deviennent alors des propriétés clefs de ces systèmes. En m’appuyant sur les développements récents du cadre mathématique de la Théorie de la viabilité que j’applique à neuf cas d’étude en productions végétales et animales, je propose ici un cadre formel pour l’évaluation de ces propriétés via des méthodes numériques. Ces travaux montrent en quoi se détacher d’une logique d’optimisation monocritère est d’autant plus pertinent que l’on s’intéresse à des systèmes écologisés, c’est-à-dire complexes, évolutifs et aux dynamiques incertaines par nature. Appréhender la viabilité de ces systèmes, demande alors non seulement de considérer leur structure (les états) mais aussi la gamme d’options de pilotage disponibles (les contrôles) permettant de se maintenir dans une gamme de situations jugées acceptables (viables) par l’agriculteur.
Cela peut impliquer d’élargir le regard porté sur le système étudié en prenant en compte l’ensemble des composantes embarquées par les objectifs de l’agriculteur, quitte à dépasser le cadre agricole strict. De la même manière cet élargissement de point de vue amène à considérer le système agricole dans son environnement en intégrant les interactions avec les autres acteurs du territoire. Ces changements d’échelle que j’envisagerai dans la suite de mes recherches engagent des questions méthodologiques pour continuer à appliquer le cadre de la viabilité à des systèmes plus vastes (de plus grandes dimensions), mais aussi pour en transposer les concepts principaux à des approches plus qualitatives.