Sous MacOS :
Prérequis :
- Installer g++ [todo]
- Installer cmake-3.13.5
Pour vérifier la version de cmake installée,
which cmake
Si ce n'est pas la bonne version, la désinstaller :
brew uninstall --force cmake
Telecharger cmake-3.13.5-Darwin-x86_64.tar.gz sur https://github.com/Kitware/CMake/releases/tag/v3.13.5
Verifier la version de cmake tékéchargée, dans le répertoire tékéchargements
ls ~/Downloads | grep cmake
doit répondre
cmake-3.13.5-Darwin-x86_64.tar
Décompresser l'archive :
tar -xvf cmake-3.13.5-Darwin-x86_64.tar
Déplacer le dossier dans le dossier viablab :
mv cmake-3.13.5-Darwin-x86_64 ~/Desktop/viablab/cmake
Vérifier la version de cmake installée :
~/Desktop/viablab/cmake/CMake.app/Contents/bin/cmake --version
doit répondre :
cmake version 3.13.5
Ajouter la commande cmake au PATH global pour l'utiliser plus facilement :
nano ~/.zshrc
Ajouter la ligne suivante à la fin du fichier :
export PATH="$HOME/Desktop/viablab/cmake/cmake-3.13.5-Darwin-x86_64/CMake.app/Contents/bin:$PATH"
Sauvegarder et quitter (appuyez sur Ctrl + X, puis Y, et enfin Entrée).
Appliquez les modifications :
source ~/.zshrc
- Installer les libriries boost [todo]
Installation de ViabLab :
[To do] #### Suivez https://viability-theory.org/node/22/ pour cloner le dossier VIABLAB ####
- Vérifier que le dossier VIABLAB/build est vide :
cd ~/VIABLAB
rm -rf build
mkdir build
- Remplacer le fichier CMakeLists.txt dans VIABLAB/source par celui-ci CMakeLists.txt
Dans le nouveau fichier CMakeLists.txt, remplacer le contenu sous ## Substitute the text within the parentheses with your ... path lignes 8, 15, 27 et 53 par vos propres chemins d'accès. - Générer le projet avec CMake depuis le dossier build
cd build
cmake -G "Unix Makefiles" -D CMAKE_BUILD_TYPE=Debug ../source
Des fichiers sont crées dans le dossier build.
Sous LINUX :
Prérequis :
Pour vérifier si g++ est installé, dans un terminal :
g++ --version
Si g++ n'est pas encore installé sur votre système :
sudo apt install g++
- Avoir installé cmake version 3.22.1 :
Pour vérifier si cmake est installé et connaitre sa version, dans un terminal :
cmake --version
Si ce n'est pas la bonne version , supprimer les versions existantes de CMake, dans un terminal :
sudo apt remove --purge cmake
Vérifier la version de votre Ubuntu, dans un terminal :
lsb_release -a
Si votre version est 22.04, installer CMake 3.22.1 automatiquement :
sudo apt update
sudo apt install cmake
Si votre version n’est pas 22.04, installer les dépendances nécessaires :
sudo apt update
sudo apt install -y build-essential libssl-dev
Télécharger CMake 3.22.1 :
wget https://github.com/Kitware/CMake/releases/download/v3.22.1/cmake-3.22.1.tar.gz
Extraire l'archive :
tar -zxvf cmake-3.22.1.tar.gz
cd cmake-3.22.1
Construire et installer :
./bootstrap
make -j$(nproc) # Compiles using all available CPU cores
sudo make install
Vérifier la version de cmake, dans un terminal :
cmake --version
Doit afficher cmake version 3.22.1.
- Avoir installé les Libraries Boost (ce sont des librairies C/C++ complémentaires, open source dont VIABLAB est dépendant):
Pour vérifier la version de Boost installée:
grep "#define BOOST_LIB_VERSION" /usr/include/boost/version.hpp
Si Boost n'est pas encore installé:
sudo apt install libboost-all-dev
Prérequis :
- Créer le dossier qui contiendra le programme et les résultats dev-cpp, créer deux sous dossier /libs et /ViablabGit, et dans /ViablabGit, un dossier /VIABLAB
- git : pour l'installer, taper dans un terminal :
sudo apt-get update
sudo apt install git
A partir du dépôt forgemia (pour les membres d'Inrae) :
Aller sur la page : https://github.com/lastre-viab/VIABLAB
Se connecter
Aller sur votre profil - Edit Profile - SSH Keys
Si le champ "Your SSH Keys" est vide :
- Générer une clé, dans un terminal, tapez
ssh-keygen
- Quand on demande un répertoire, on peut laisser vide, un répertoire est créé automatiquement
- Entrer une phrase à mémoriser
- Dans le répertoire créé, deux fichiers sont créés, copier le contenu du fichier .pub
Cliquer sur "Add new key"
Coller dans le champ "Your SSH Keys"
Cliquer sur "Add key".
Dans un terminal,
git clone git@forgemia.inra.fr:lisc/VIABLAB.git <nom du dossier (sinon sera copié dans le dossier courant>
Choisir la branche que l'on souhaite utiliser (celle de Matéu est my_branch) avec
git checkout my_branch
Dans le répertoire VIABLAB/, créer le répertoire build
mkdir build
Si pas de cmake, (pour vérifier taper cmake --version), il faut installer cmake :
brew install cmake
MAIS il semble y avoir un problème de version, la commande précédente a installé une version 4..... il semblerait qu'il faille utiliser une version au plus 3....
cmake -S source/ - B build/
Sous WINDOWS :
Prérequis :
- Avoir créé le dossier qui contiendra le programme et les résultats dev-cpp, créer deux sous dossier /libs et /ViablabGit, et dans /ViablabGit, un dossier /VIABLAB
- Avoir installé git-for-Windows :
Aller à l'adresse https://git-scm.com/downloads/win
Cliquer sur: Click here to download
Exécuter le fichier téléchargé et choisir toutes les options par defaut.
- Avoir installé MinGW, une distribution de compilateurs C/C++ GNU pour Windows :
A l'adresse https://sourceforge.net/projects/mingw/files/latest/download , téléchargez l'application MinGW Installation Manager.
Ouvrir cette application
Dans le panneau gauche, développer All packages => MinGW, sélectionner MinGW Base System. Sélectionner dans la liste des packages tous les packages dont le nom contient « pthread », choisir Mark For Installation. Faire de même pour les packages gcc, omp, g++, libstd, mingw s’ils ne sont pas sélectionnés.
Une fois les packages sélectionnés, dans le menu Installation, cliquer sur Apply changes et attendre la fin d’installation.
Ajouter l’emplacement de l’installation MinGW dans la variable PATh du système :
Dans paramètres/settings du système, on cherche environmental/environnement et on clique dans «edit environment variables for your account »
Aller dans Path, edit, new et on copie colle : C:\MinGW\bin
Eteindre et redémarrer l'ordinateur.
- Avoir installé cmake version 3.31.7:
Pour vérifier si cmake est installé et connaitre sa version, dans un terminal :
??
Si ce n'est pas la bonne version , supprimer les versions existantes de CMake, dans un terminal :
??
Aller à l'adresse https://github.com/Kitware/CMake/releases/download/v3.31.7/cmake-3.31.7-windows-x86_64.msi pour télécharger le Windows x64 installer.
Vérifier la version de cmake, dans un terminal :
????
Doit afficher cmake version 3.31.7.
- Avor installé boost, les Libraries Boost sont nécessaires, ce sont des librairies C/C++ complémentaires, open source dont VIABLAB est dépendant.
- Avoir installé Eclipse Environnement de développement intégré) (facultatif) :
Aller à l'adresse https://www.eclipse.org/downloads/packages/release/kepler/sr2/eclipse-ide-cc-developers
Cliquer sur download, à nouveau sur download.
Une fois téléchargé, cliquer sur l’installeur et chosir Eclipse IDE for C/C++ developers
On ‘’launch’’ par la suite (première exécution pour voir que tout fonctionne)
On ‘’launch’’ de nouveau.
Installation de Viablab :
- A l'adresse, https://github.com/lastre-viab/VIABLAB/releases/tag/v3.0
- Télécharger InstallerViabLabGui_Win.exe
- Pour rendre le fichier exécutable
??
- Pour exécuter l'installeur
??
- Next - Next - Next - Install - Finish
- Puis ouvrir un PowerShell, se placer à l’aide de la commande cd dans le répertoire build : ~/ViabLabGui/bin/VIABLAB/build
- puis, pour une utilisation sans l'IDE Eclipse :
cmake -G "MinGW Makefiles" ../source
- ou, pour une utilisation avec Eclipse :
cmake -G"Eclipse CDT4 - MinGW Makefiles" -D CMAKE_BUILD_TYPE=Debug ../source
Après l’exécution de cmake le projet est prêt pour être importé dans Eclipse : le répertoire build ( vide au début) contient les données générées par cmake.
Dans Eclipse, aller dans le menu File => Import et sélectionner l’option Existing Projects into Workspace
Cliquer sur Next
Ensuite dans le fenêtre suivante sélectionner le répertoire build
Cliquer sur Finish
Après l’import on voit l’arborescence du projet dans le panneau gauche

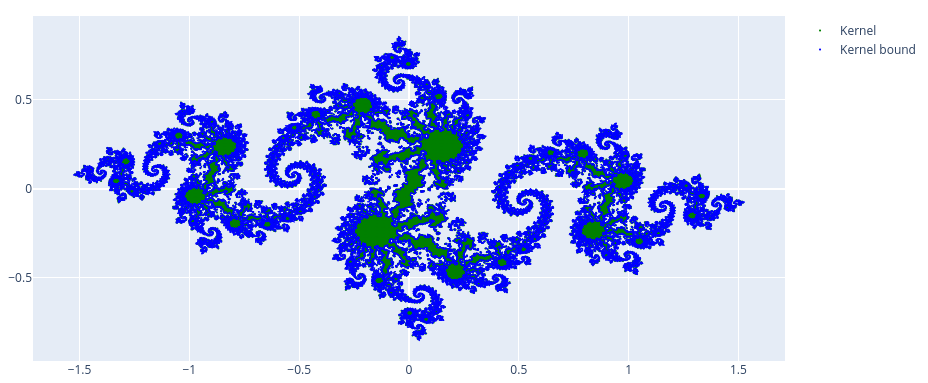
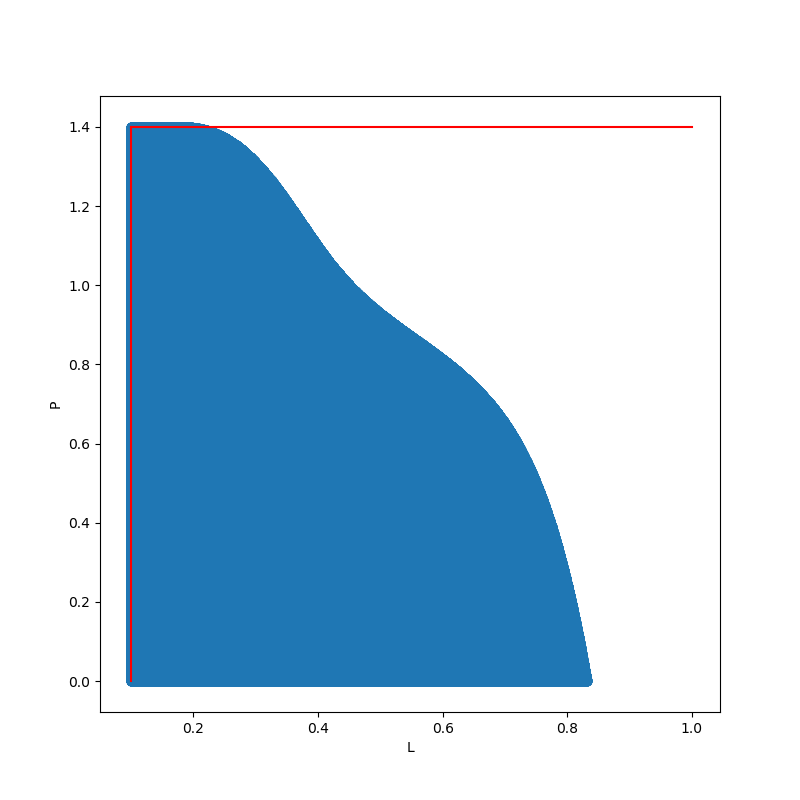
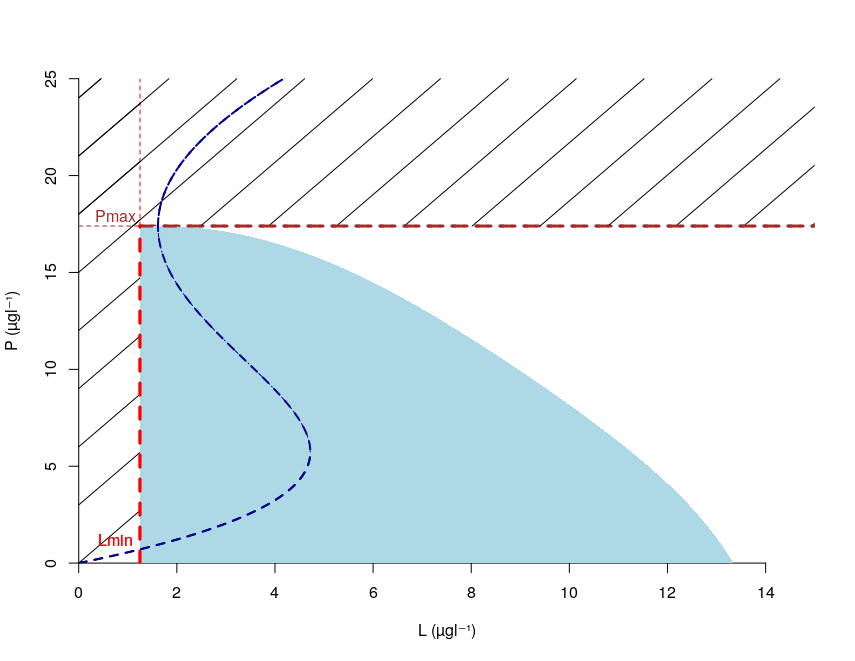 In light blue the viabillity kernel. The dotted marine line shows the equilibrium curve of the system.
In light blue the viabillity kernel. The dotted marine line shows the equilibrium curve of the system.